Как эффективность обходчика влияет на тестирование
Используемый в тестах, построенных по технологии UniTESK, обходчик позволяет осуществить полный перебор возможных тестовых ситуаций путем вызова всевозможных тестовых воздействий во всех состояниях графа, заданного в неизбыточном виде. Таким образом, могут быть получены последовательности тестовых воздействий, которые практически никогда не проверяются при ручном построении тестов.
Может показаться, что для разработки хорошего теста достаточно указать набор сценарных функций и определить функцию вычисления состояния, и после этого обходчик все сделает сам. В общем случае это неверно. Неправильно выбранный метод обхода, неправильные ограничения на количество состояний, неправильное определение состояния графа: все это может привести к невозможности получения результата в условиях ограниченности ресурсов.
Возникает следующая проблема: ошибка может проявиться в последовательности тестовых воздействий, состоящей из сотни переходов по дугам графа, но выбранный механизм обхода будет не в состоянии обеспечить достижения подобной ситуации, по причине того, что он неудачно использует полный перебор.
Пример. Если человек находится на улице у дома номер 1, и хочет дойти к дому номер 91, то он может пойти прямо и дойти до цели. Действуя иначе, он может поворачивать на любом перекрестке, стараясь не проходить по два раза по одному и тому же кварталу. По дороге он увидит много интересного, но к цели придет с колоссальным запозданием.
Из этого следует, что строить обход графа, заданного в неизбыточном виде, нужно аккуратно. При неосмотрительном использовании перебора всех возможных вариантов в сложных ситуациях могут возникнуть трудности.
Поэтому детали реализации алгоритма обходчика имеют большое значение для эффективности тестирования больших систем. Очевидно, что построить обход всех дуг графа можно различными путями, необязательно эквивалентными по эффективности использования памяти и времени. Приведем несколько примеров.
«Цепной» пример. Описываемая в этом примере ситуация возникает в тех случаях, когда состоянием системы является целое число, и доступны два вида тестовых воздействий: увеличивающее и уменьшающее значение состояния на единицу.
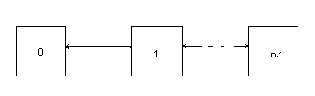
Рисунок 1.Граф состояний и переходов для «цепного» примера.
В этом случае возможен обход вида (перечисляются состояния в порядке их посещения) 0, 1, 0, 1, 2, 1, 0, …, 0, 1, 2, …, (n-2), (n-1), (n-2), …, 1, 0.
Также возможен обход вида 0, 1, 2, …, (n-2), (n-1), (n-2), …, 1, 0.
В обоих случаях проходятся все дуги во всех состояниях графа, однако в первом случае количество тестовых воздействий, проделанных при обходе, равно 2n(n+1)/2 = n(n+1), тогда как во втором оно составляет только 2n.
Из приведенного примера вытекает следующая рекомендация по работе обходчика: в случае наличия непройденных дуг из текущего состояния графа, обходчику рекомендуется первой вызывать операцию, соответствующую одной из этих непройденных дуг.
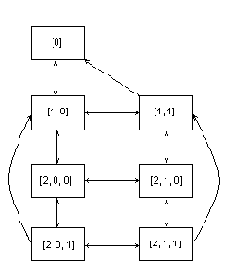
То есть, не рекомендуется переходить к вызову сценарной функции B, пока не исчерпаны возможные вызовы сценарной функции A. При этом порядок задания сценарных функций, определяющий последовательность их вызова обходчиком, должен тщательно обдумываться разработчиком тестов для определения максимально эффективного обхода. Примеры с потоками. Приведенные ниже примеры выбраны из-за высокой степени связности графов, а также относительно малого количества состояний и дуг, что позволяет понять существо проблемы, не рассматривая сложные случаи. О том, что такое поток (thread) и обработчик завершения потока (cleanup handler) можно прочесть в [] и [] соответственно. Простой пример с потоками. Граф состояний и переходов простой модели системы управления потоками, описываемой в стандарте POSIX [], изображен на Рисунке 2. В этой модели разрешается иметь не более одного потока одновременно.
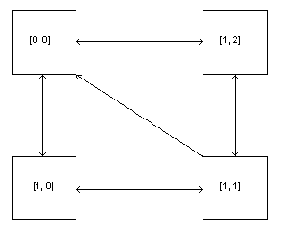
Он соответствует последовательности сценарных функций CKUO. Сложный пример с потоками. Рассмотрим более сложную модель той же системы, допуская уже два активных потока.